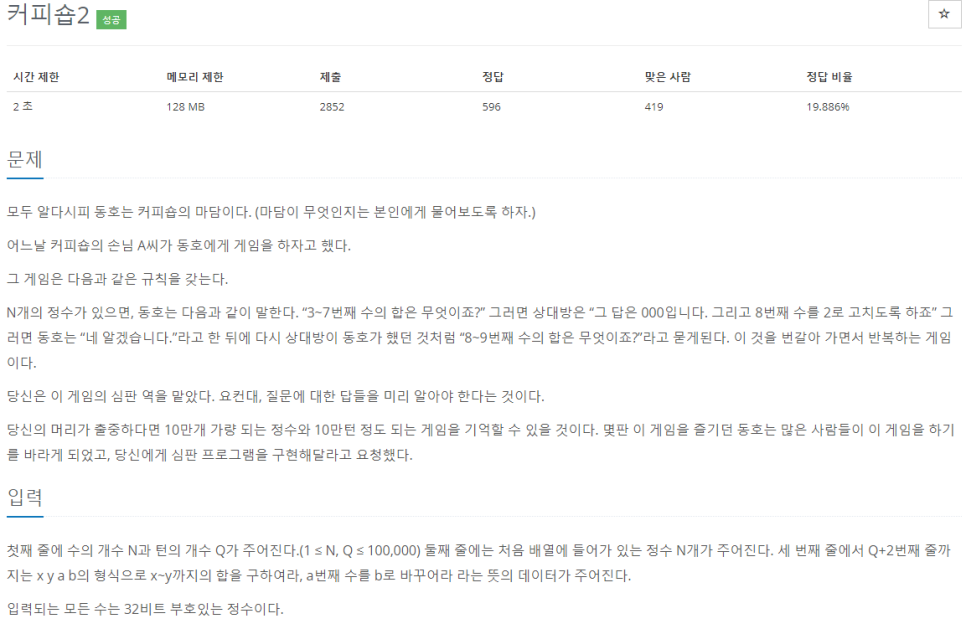
중복값 처리와 배열 초기화 때문에 굉장히 애먹은 문제이다....

접근한 방식은 입력받은 하나의 수열값들을 인덱싱을 통해 표시를 해주고(음수값 + 고정 Value처리)

나머지 하나의 수열을 입력받으면서

교차점일 경우에 해당 인덱스 지점까지의 Prefix_Sum값을 비교해주는 것이다. 
(before 교차점까지의 PrefixSum의 차이값 비교)

하지만... 인덱싱 처리해준 값들을 여러테케를 돌리는 문제이다보니 

초기화 해주지 않은 것이 화근이었다...ㅠ

좀더 꼼꼼할 필요가 있는 자신을 돌아보게됨..

스티커 이미지

https://www.acmicpc.net/problem/4929

<Code>

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
//pda_pro12
#include<algorithm>
#include<iostream>
#include<vector>
 
#define N_ 10001
#define sz(x) x.size()
using namespace std;
 
typedef long long ll; 
typedef double db; 
int a[N_], a1[N_], Prefix[N_], Prefix1[N_], n, m, Num[20002], Sum1, Sum2, ans, before, before1;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    while (cin >> n && n > 0) {
        ans = 0;  before = 0; before1 = 0;
        for (int i = 1; i <= n; i++) {
            cin >> a[i]; Num[a[i] + 10000] = i;
            Prefix[i] = a[i];
            Prefix[i] += Prefix[i - 1];
        }
        cin >> m;
        for (int i = 1; i <= m; i++) {
            cin >> a1[i];
            Prefix1[i] = a1[i];
            Prefix1[i] += Prefix1[i - 1];
            if (Num[a1[i] + 10000]) {
                int lower_Sum = Num[a1[i] + 10000];
                Sum1 = Prefix[lower_Sum] - Prefix[before];
                Sum2 = Prefix1[i] - Prefix1[before1];
                before1 = i; before = lower_Sum;
                ans += (Sum1 > Sum2) ? Sum1 : Sum2;
            }
        }
        int r = Prefix[n] - Prefix[before];
        int q = Prefix1[m] - Prefix1[before1];
        ans += (r > q) ? r : q;
        cout << ans << '\n';
        for (int i = 0; i <= 20000; i++)
            Num[i] = 0; 
    }
    return 0;
}


저작자표시

'PS) BOJ > Binary Search' 카테고리의 다른 글

[C++] 랜선 자르기 [BOJ 1654]  (0) 2018.08.16
[C++] K번째 수[백준 1300]  (0) 2018.08.16
[C++] 게임 [백준 1072]  (0) 2018.08.16
[C++]입국심사[백준 3079]  (0) 2018.08.15

문제를 살펴보면 딱히 어려운 문제는 아니다. 

그냥 다익스트라 2차원으로 돌리면된다. 

흰색이 1 검은색이 0이라는 점에 착안하면 검은색에 가중치를 두기 위해 필자는 원본을 toggle 해줬다. 

그냥 벡터도 필요없이 dst 2차원을 갱신해주며 다익스트라를 돌려주자
(요즘 너무 쉬운것만 올리는것 같다 - 맨날 이소리하고 맨날 쉬운거 올린다)

https://www.acmicpc.net/problem/2665

2665번: 미로만들기
2665번 제출 맞은 사람 숏코딩 풀이 풀이 작성 풀이 요청 재채점/수정 채점 현황 강의 미로만들기 시간 제한 메모리 제한 제출 정답 맞은 사람 정답 비율 1 초 128 MB 2961 1257 858 42.644% 문제 n×n 바둑판 모양으로 총 n 2 개의 방이 있다. 일부분은 검은 방이고 나머지는 모두 흰 방이다. 검은 방은 사면이 벽으로 싸여 있어 들어가 수 없다. 서로 붙어 있는 두 개의 흰 방 사이에는 문이 있어서 지나다닐 수 있다. 윗줄 맨 왼쪽 방은 시작방으로서 항상 흰 방이고, 아랫줄 맨 오른쪽 방은 끝방으
www.acmicpc.net

<Code>

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// pda_pro12
#include<iostream>
#include<algorithm>
#include<queue>
#include<stdio.h>
 
#define INT 0x7fffffff
#define N_ 51
 
using namespace std;
 
int n, a[N_][N_], dst[N_][N_], dx[] = { -1,1,0,0 }, dy[] = { 0,0,1,-1 };
priority_queue<pair<pair<int, int>, int>> pq;
 
int main() {
    cin >> n;
    for (int i = 0; i < n; i++){
        for (int j = 0; j < n; j++){
            scanf("%1d", &a[i][j]);
            a[i][j] = (a[i][j] == 0) ? 1 : 0; 
            dst[i][j] = INT;
        }
    }
    dst[0][0] = 0;
    pq.push({ {0,0},0 });
    while (!pq.empty()) {
        int v_x = pq.top().first.first; int v_y = pq.top().first.second;
        int dis = -pq.top().second;
 
        pq.pop();
        if (dis > dst[v_x][v_y]) continue;
        for (int i = 0; i < 4; i++) {
            int nx = v_x + dx[i]; int ny = v_y + dy[i]; 
            if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue; 
            int n_dis = dis + a[nx][ny]; 
            if (n_dis < dst[nx][ny]) {
                dst[nx][ny] = n_dis; 
                pq.push({ {nx, ny}, -n_dis });
            }
        }
    }
    cout << dst[n - 1][n - 1]; 
    return 0;
}


저작자표시

'PS) BOJ > Disjoint_set' 카테고리의 다른 글

[C++] 네트워크 연결 [백준 3780]  (0) 2018.08.17
[C++] 공항 [BOJ 10775]  (0) 2018.08.17

전형적인 세그먼트 트리 문제인데 함정은 쿼리에 무조건 작은수~큰수라는 조건이 없으므로 
조건으로 잘 처리해주면 금방 풀수 있는 문제이다. 
바텀업 세그먼트 트리를 구현해서 풀었다. 

구간합 구하기 문제는 역시 세그먼트 트리 구현해서 푸는게 짱인거같다...
(내가 아는선에서는... ㅎ)

시간복잡도는 M*NlogN 만큼 소요되는것같다. 
주어지는 쿼리의 수가 10만턴정도이니 입출력을 줄여주는것도 시간을 충분히 줄여준다. 

참고로 덧셈과정에서 정수형을 넘어갈수 있으니 long long을 사용했다.


https://www.acmicpc.net/problem/1275

1275번: 커피숍2
1275번 제출 맞은 사람 숏코딩 풀이 풀이 작성 풀이 요청 재채점/수정 채점 현황 강의 커피숍2 시간 제한 메모리 제한 제출 정답 맞은 사람 정답 비율 2 초 128 MB 2852 596 419 19.886% 문제 모두 알다시피 동호는 커피숍의 마담이다. (마담이 무엇인지는 본인에게 물어보도록 하자.) 어느날 커피숍의 손님 A씨가 동호에게 게임을 하자고 했다. 그 게임은 다음과 같은 규칙을 갖는다. N개의 정수가 있으면, 동호는 다음과 같이 말한다. “3~7번째 수의 합은 무엇이죠?” 그러면 상대방은
www.acmicpc.net

<CODE>


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
//pda_pro12
#include<algorithm>
#include<iostream>
 
#define N_ 100000
#define INT 0x7fff0000
 
using namespace std; 
 
typedef long long ll;
ll a[N_], seg[N_ * 4], n, q; 
 
void init(int node, int x, int y) {
    if (x == y) {
        seg[node] = a[x]; 
        return; 
    }
    int mid = (x + y) >> 1; 
    init(node << 1, x, mid); 
    init((node << 1) + 1, mid + 1, y); 
    seg[node] = seg[node << 1] + seg[(node << 1) + 1];
    return; 
}
 
void update(int pos, int val, int node, int x, int y) {
    if (pos < x || pos > y) return; 
    if (x==y) {
        seg[node] = val; 
        return; 
    }
    ll mid = (x + y) >> 1; 
    update(pos, val, node << 1, x, mid); 
    update(pos, val, (node << 1) + 1, mid + 1, y); 
    seg[node] = seg[node << 1] + seg[(node << 1) + 1]; 
    return; 
}
 
ll query(int lo, int hi, int node, int x, int y) {
    if (lo > y || hi < x) return 0; 
    if (lo <= x && y <= hi) return seg[node]; 
    ll mid = (x + y) >> 1; 
    ll l = query(lo, hi, node << 1, x, mid); 
    ll r = query(lo, hi, (node << 1) + 1, mid + 1, y);
    return l+r; 
}
 
int main() {
    ios::sync_with_stdio(false); 
    cin.tie(NULL); 
    cout.tie(NULL); 
 
    cin >> n >> q; 
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    init(1, 1, n); 
    while (q--) {
        int a, b, c, d; 
        cin >> a >> b >> c >> d;
        int a1 = (a > b) ? b : a; int b1 = (a > b) ? a : b; 
        cout << query(a1, b1, 1, 1, n) << '\n'; 
        update(c, d, 1, 1, n);
    }
    return 0; 
}


저작자표시

'PS) BOJ > Segment Tree' 카테고리의 다른 글

[C++] 커피숍2 [백준 1275]  (0) 2018.08.16
[C++]음주 코딩[백준 5676]  (0) 2018.08.16

Disjoint_Set의 개념으로 길이 배열을 한가지 더 선언해주어서 절대 차이만큼만 

더해주면서 저장하면 되는 것이었다. 

find 와 init 과정에서 parent 배열과 길이를 저장할 배열을 따로 만들어주었다. 

find를 호출할때마다 해당 노드의 루트노드를 탐색하고 루트노드까지의 길이를 해당 인덱스의

길이 배열에 저장해주었다. 

(어렵게 생각하기보단 풀리지 않는다면 Disjoint_set의 과정을 완벽히 이해해보시길 바랍니다.)

그래도 이해가 가지않는다면 댓글과 쪽지를 주세요!

스티커 이미지

https://www.acmicpc.net/problem/3780

3780번: 네트워크 연결
문제 종빈이는 아주 큰 그룹의 총수다. 이 그룹은 1부터 N번까지의 번호로 구분할 수 있는 N개의 기업을 운영하고 있다. 현재 각 기업은 서로 독립적인 자체 컴퓨팅 및 통신센터를 가지고 있다. 어느 날 종빈이는 계열사의 CTO인 서현이에게 서비스 개선을 위해 각 기업의 서버를 네트워크로 연결하여 단일 통신센터에서 관리 가능한 클러스터 형태로 구성할 것을 제안했다. 종빈이의 제안을 들은 서현이는 다음과 같은 병합 과정을 고안해냈다. 클러스터 A를 제공하는 기존에 존재하는 센터 I를 고른다. 클러스터 B를 제공하는 기업 J를 고른다.
www.acmicpc.net

<CODE>


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
//pda_pro12
#include<iostream>
#include<algorithm>
 
#define sz(x) x.size()
#define all(x) x.begin(), x.end()
#define N_ 20001
#define mod (int)1e3
 
using namespace std;
 
typedef long long ll;
typedef pair<int, int> pll;
typedef double db;
 
int n, m, t, par[N_], len[N_];
 
void init() {
    for (int i = 1; i <= n; i++)
        par[i] = i, len[i] = 0;
    return;
}
 
int find(int x) {
    if (x == par[x])
        return x;
    else {
        int tmp = find(par[x]); 
        len[x] += len[par[x]]; 
        par[x] = tmp; 
        return tmp;
    }
}
 
void Merge(int x, int y) {
    len[x] = abs(x - y) % mod; 
    par[x] = y; 
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    cin >> t;
    while (t--) {
        cin >> n;
        init(); 
        char inp; int a, b;
        while (1) {
            cin >> inp;
            if (inp == 'O')
                break; 
            else if (inp == 'E') {
                cin >> a;
                find(a); 
                cout << len[a] << '\n';
            }
            else if (inp == 'I') {
                cin >> a >> b;
                Merge(a, b);
            }
        }
    }
    return 0;
}


저작자표시

'PS) BOJ > Disjoint_set' 카테고리의 다른 글

[C++]미로 만들기 [BOJ 2665]  (0) 2018.08.21
[C++] 공항 [BOJ 10775]  (0) 2018.08.17


굉장히 간단한 문제를 조건하나를 빠트려서 계속 헛다리 짚은 문제이다...
( 내시간... )

n번 게이트에 도킹 되면 가장 인접하면서 낮은 번호의 게이트로 도킹이 되고, 연결해야할 게이트가 
0번 밖에 남지 않았다고 한다면 마쳐주면된다. 

도킹 게이트가 0임을 포착한 순간 바로 입력하던 반복문도 빠져나오고 현 게이트 수를 출력하고 종료시켜줘야한다. 
(이거때매 30분넘게 해맸다...)

https://www.acmicpc.net/problem/10775

<CODE>


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//pda_pro12
#include<iostream>
#define N_ 100001
 
using namespace std;
 
int g, p, par[N_], inp, cnt;
 
void init() {
    for (int i = 1; i <= g; i++)
        par[i] = i;
    return;
}
 
int find(int x) {
    if (x == par[x])
        return x;
    return par[x] = find(par[x]);
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
 
    cin >> g >> p;
    init();
    for (int i = 1; i <= p; i++) {
        cin >> inp;
        if (find(inp) == 0) {
            break;
        }
        if (find(inp)) {  // 내가 도킹하려는 곳이 가능한지 확인 
            cnt++;
            par[find(inp)] = find(find(inp) - 1);
        }
    }
    cout << cnt << '\n';
    return 0;
}


저작자표시

'PS) BOJ > Disjoint_set' 카테고리의 다른 글

[C++]미로 만들기 [BOJ 2665]  (0) 2018.08.21
[C++] 네트워크 연결 [백준 3780]  (0) 2018.08.17

올 초에 이분탐색 개념을 처음 알았을때 어떻게 이분탐색을 꾸역꾸역 끼워넣을지 고민했던 기억이...

생각해보면 무척 간단한거였다. 

문제 해결과정

1. 랜선의 길이의 상한과 하한을 잡아준다. 

2. 랜선의 하한과 상한을 기준으로 중간값을 구해주고 중간값을 길이로 가정하고 몇개의 랜선으로 쪼개  
   질수 있는지 탐색해본다.

<직접 손으로 써서 설명해봤는데 이해가 잘될지 모르겠다>

이렇게 탐색하면 1~최대 2147483647이니깐  NLogK만 끝낼수 있다 
(가정된 길이에 대한 갯수 구하는과정)N*LogK

(상한 하한의 길이만큼을 /2해가면서 탐색하므로 Log길이 만큼이된다.)

https://www.acmicpc.net/problem/1654


<Code>

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//pda_pro12
#include<algorithm>
#include<iostream>
#define N_ 10001
#define INT 0x7fff0000
using namespace std;
 
typedef long long ll; 
int k, n, a[N_], Max;    ll lft, rgt; 
int main() {
    ios::sync_with_stdio(false); 
    cin.tie(NULL); 
    cout.tie(NULL); 
 
    cin >> k >> n; 
    for (int i = 0; i < k; i++) 
        cin >> a[i], Max = max(a[i],Max);             // 보유중인 랜선에 대한 정보를 입력받음 
    int ans = 0; 
    lft = 1;  rgt = Max; 
    while (lft <= rgt) {
        ll mid = (lft + rgt) >> 1; 
        int Sum = 0; 
        for (int i = 0; i < k; i++) 
            Sum += (a[i] / mid); 
        if (Sum >= n) 
            ans = mid,lft = mid + 1;
        else
            rgt = mid - 1; 
    }
    cout << ans; 
    return 0; 
}


저작자표시

'PS) BOJ > Binary Search' 카테고리의 다른 글

[C++]수열 걷기[백준 4929]  (0) 2018.08.21
[C++] K번째 수[백준 1300]  (0) 2018.08.16
[C++] 게임 [백준 1072]  (0) 2018.08.16
[C++]입국심사[백준 3079]  (0) 2018.08.15

이분탐색을 시작하는 분들도 쉽게 풀만한 문제라고 생각된 문제중 하나였다. 

배열 A[i][j] = i*j라는 특성을 사용해서 결국 행*열의 곱이라는 말이다. 굳이 일차원배열로 늘어놓고

정렬을 안해도되고, 하게된다면 시간초과의 난관을 겪을 것이다. 

예를들어보자 n이 5일때 1*1, 1*2, 1*3, 1*4, 1*5, 2*1, ... 이다.

6이라는 수를 가정하고 몇번째 수인지 따저본다. 1행에서 6보다 작은수는 6/1 즉 6개 

2행에서는  6/ 2 = 3개 이런식이다. 실제로 2,1   2,2    2,3 이렇게 3개인것이다. 

따라서 그냥 lft를 1로 설정하고 k번째 수가 절대 k보다 클리는 없으므로 k로 상한을 잡고 

이분탐색을 돌리면 되는것이다. 

실제로 풀어보면 이분탐색에 대한 자신감이 팍팍 솟는 문제!


1300번: K번째 수
1300번 제출 맞은 사람 숏코딩 풀이 풀이 작성 풀이 요청 재채점/수정 채점 현황 강의 K번째 수 시간 제한 메모리 제한 제출 정답 맞은 사람 정답 비율 2 초 128 MB 2495 772 567 35.130% 문제 세준이는 N*N크기의 배열을 만들었다. (배열의 방 번호는 1부터 시작한다.) 그 배열을 A라고 했을 때, 배열에 들어가는 수는 A[i][j] = i*j 이다. 세준이는 이 수를 일차원 배열 B에 넣으려고 한다. 그렇게 되면, B의 크기는 N*N이 될 것이다. 그러고 난 후에, B를 정렬해서 k번째 원소를 구하려고 한
www.acmicpc.net

https://www.acmicpc.net/problem/1300

<Code>

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// pda_pro12
#include<algorithm>
#include<iostream>
#define N_ 100000
using namespace std; 
typedef long long ll; 
 
int a, b, ans; ll lft, rgt; 
 
int main() {
    cin >> a >> b;
 
    lft = 1;  rgt = b; 
 
    while (lft <= rgt) {
        int mid = (lft + rgt) >> 1;   // 가정된 K번째 
        ll Sum = 0; 
        for (int i = 1; i <= a; i++)    // 행마다 mid보다 작은수의 갯수를 측정
            Sum += min(a, mid / i); 
        if (Sum >= b)
            rgt = mid - 1, ans = mid;
        else
            lft = mid + 1; 
    }
    cout << ans; 
    return 0; 
}


저작자표시

'PS) BOJ > Binary Search' 카테고리의 다른 글

[C++]수열 걷기[백준 4929]  (0) 2018.08.21
[C++] 랜선 자르기 [BOJ 1654]  (0) 2018.08.16
[C++] 게임 [백준 1072]  (0) 2018.08.16
[C++]입국심사[백준 3079]  (0) 2018.08.15

아이디어 도출해놓고 자료형 실수와 오버플로우를 예측하지 못해 30분동안 삽질한...문제였다...

먼저 향상된 게임실력으로 더이상 지지않는다는 전재가 있으므로 

확률 z = (y(이긴 게임 수)/x(총게임수))*100 이 바뀌기 위해 추가로 진행해야하는 최소의 게임수를 

구하는 문제이다. 최소의 게임수라는 말은 없지만 확률이 변하는 순간의 게임수이므로 최소의 게임

수를 구하면 된다. 

문제 풀이 순서

1. 하한을 0게임으로 잡고 상한을 1000000001로 잡았다(상한 잘못 잡아서 고생했다...)

2. 이분탐색으로 (하한+상한)/2만큼 추가게임을 진행하였을때의 확률을 계산하여 확률이 변하였는지
   확인해본다. 

3. 확률이 변했다면 상한값을 줄이고, 변하지 않았다면 하한값을 중간값+1방식으로 늘려간다. 

4. 이렇게 left <= right를 만족할때까지 진행되므로 결국 하한에 수렴하도록 mid를 설정하고 검사한
     다.

5. 빠저나왔을때의 left값은 확률이 변하는 순간의 하한이다.

자료형과 범위에서 실수로 고생한걸 보면서 한참 멀었구나를 느꼇다...

https://www.acmicpc.net/problem/1072

<Code>


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
// pda_pro12
#include<algorithm>
#include<iostream>
 
#define INT 0x7fff0000
#define MAX_ 1000000001
 
using namespace std;
 
typedef long long ll;
ll x, y, z; ll lft, rgt;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
 
    while (cin >> x >> y) {
        z = y * 100 / x;
        lft = 0;  rgt = MAX_;
        int ans = z;
        while (lft <= rgt) {
            ll mid = (lft + rgt) >> 1;  // 추가 게임횟수 
            ll per = (y + mid) * 100 / (x + mid);
            if (per > z) {
                rgt = mid - 1;
            }
            else
                lft = mid + 1;
        }
        if (lft >= MAX_) {
            cout << -1 << '\n';
        }
        else
            cout << lft << '\n';
    }
    return 0;
}


저작자표시

'PS) BOJ > Binary Search' 카테고리의 다른 글

[C++]수열 걷기[백준 4929]  (0) 2018.08.21
[C++] 랜선 자르기 [BOJ 1654]  (0) 2018.08.16
[C++] K번째 수[백준 1300]  (0) 2018.08.16
[C++]입국심사[백준 3079]  (0) 2018.08.15

전형적인 세그먼트 트리 문제인데 함정은 쿼리에 무조건 작은수~큰수라는 조건이 없으므로 
조건으로 잘 처리해주면 금방 풀수 있는 문제이다. 
바텀업 세그먼트 트리를 구현해서 풀었다. 

구간합 구하기 문제는 역시 세그먼트 트리 구현해서 푸는게 짱인거같다...
(내가 아는선에서는... ㅎ)

시간복잡도는 M*NlogN 만큼 소요되는것같다. 
주어지는 쿼리의 수가 10만턴정도이니 입출력을 줄여주는것도 시간을 충분히 줄여준다. 

참고로 덧셈과정에서 정수형을 넘어갈수 있으니 long long을 사용했다.

스티커 이미지

https://www.acmicpc.net/problem/1275

1275번: 커피숍2
1275번 제출 맞은 사람 숏코딩 풀이 풀이 작성 풀이 요청 재채점/수정 채점 현황 강의 커피숍2 시간 제한 메모리 제한 제출 정답 맞은 사람 정답 비율 2 초 128 MB 2852 596 419 19.886% 문제 모두 알다시피 동호는 커피숍의 마담이다. (마담이 무엇인지는 본인에게 물어보도록 하자.) 어느날 커피숍의 손님 A씨가 동호에게 게임을 하자고 했다. 그 게임은 다음과 같은 규칙을 갖는다. N개의 정수가 있으면, 동호는 다음과 같이 말한다. “3~7번째 수의 합은 무엇이죠?” 그러면 상대방은
www.acmicpc.net


<Code>


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
//pda_pro12
#include<algorithm>
#include<iostream>
 
#define N_ 100000
#define INT 0x7fff0000
 
using namespace std; 
 
typedef long long ll;
ll a[N_], seg[N_ * 4], n, q; 
 
void init(int node, int x, int y) {
    if (x == y) {
        seg[node] = a[x]; 
        return; 
    }
    int mid = (x + y) >> 1; 
    init(node << 1, x, mid); 
    init((node << 1) + 1, mid + 1, y); 
    seg[node] = seg[node << 1] + seg[(node << 1) + 1];
    return; 
}
 
void update(int pos, int val, int node, int x, int y) {
    if (pos < x || pos > y) return; 
    if (x==y) {
        seg[node] = val; 
        return; 
    }
    ll mid = (x + y) >> 1; 
    update(pos, val, node << 1, x, mid); 
    update(pos, val, (node << 1) + 1, mid + 1, y); 
    seg[node] = seg[node << 1] + seg[(node << 1) + 1]; 
    return; 
}
 
ll query(int lo, int hi, int node, int x, int y) {
    if (lo > y || hi < x) return 0; 
    if (lo <= x && y <= hi) return seg[node]; 
    ll mid = (x + y) >> 1; 
    ll l = query(lo, hi, node << 1, x, mid); 
    ll r = query(lo, hi, (node << 1) + 1, mid + 1, y);
    return l+r; 
}
 
int main() {
    ios::sync_with_stdio(false); 
    cin.tie(NULL); 
    cout.tie(NULL); 
 
    cin >> n >> q; 
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    init(1, 1, n); 
    while (q--) {
        int a, b, c, d; 
        cin >> a >> b >> c >> d;
        int a1 = (a > b) ? b : a; int b1 = (a > b) ? a : b; 
        cout << query(a1, b1, 1, 1, n) << '\n'; 
        update(c, d, 1, 1, n);
    }
    return 0; 
}


저작자표시

'PS) BOJ > Segment Tree' 카테고리의 다른 글

[C++] 커피숍2 [백준 1275]  (0) 2018.08.17
[C++]음주 코딩[백준 5676]  (0) 2018.08.16

인덱스 범위가 10만이고 인덱스마다 값의 범위는 -100~100인 배열을 입력으로 주고, 

구간을 갱신, 합산출을 M만큼 해주는건데 K의 범위또한 10만이다. 

(즉, -> Prefix_Sum을 사용하거나 세그먼트를 써야한다는건데 갱신이 있으므로 세그먼트를 썻다.)

시간복잡도는 대략 O(KlogN) 인것 같다. 

구현한 세그먼트는 바텀-업 세그먼트를 사용하였다

처음 풀때 실수 했던게 10만개의 인덱스가 전부 100을 갖고 있을때는 곱셈연산이므로 

100의 10만승이라는 1Googol을 훌쩍 넘어버리는.. 수가 발생한다는 것을 뒤늦게 알고, 

( 참고로 1구골이  10의 100승이다 ) 


세그트리를 구축해주는 함수에서 음, 양, 0을 판별하고 부분곱 방식으로 트리를 쌓아올렸다. 

스티커 이미지

그래도 실행시간은 나쁘지 않게 나와서 좀 만족스럽다 ㅎㅎㅎ

https://www.acmicpc.net/problem/5676

5676번: 음주 코딩
문제 오늘은 ACM-ICPC 대회 전 날이다. 상근이는 긴장을 풀기 위해서 팀원들과 근처 술집으로 갔다. 상근이와 친구들은 다음 날 있을 대회를 연습하기 위해서 작은 게임을 하기로 했다. 먼저, 선영이는 상근이에게 총 N개의 정수로 이루어진 수열 X 1 , X 2 , ... X N 을 적어준다. 게임은 총 K번 라운드로 이루어져있고, 매 라운드마다 선영이는 상근이에게 명령을 하나씩 내린다. 명령은 아래와 같이 두 가지가 있다. 변경: 이 명령은 친구가 수열의 한 값을 바꾸고 싶을 때 사용한다. 곱셈: 선영이는 상근이에게 i와 j를
www.acmicpc.net


<Code>


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
// pda_pro12
#include<algorithm>
#include<iostream>
#define N_ 100001   // 수열의 최대 크기 
#define INT 0x7fff0000
 
using namespace std; 
 
typedef long long ll; 
int seg[N_ * 4], a[N_], t, n, m, k;
 
void init(int node, int x, int y) {
    if (x == y) {
        if (a[x] > 0) seg[node] = 1; 
        else if (a[x] == 0) seg[node] = 0; 
        else if (a[x] < 0)  seg[node] = -1; 
        return; 
    }
    int mid = (x + y) >> 1; 
    init(node << 1, x, mid); 
    init((node << 1) + 1, mid + 1, y); 
    seg[node] = seg[node << 1] * (seg[(node << 1) + 1]); 
    return; 
}
 
void update(int pos, int val, int node, int x, int y) { 
    if (pos < x || pos > y) return; 
    if (x == y) {
        if (val > 0) seg[node] = 1;
        else if (!val) seg[node] = 0; 
        else if (val < 0) seg[node] = -1; 
        return; 
    }
    int mid = (x + y) >> 1; 
    update(pos, val, node << 1, x, mid); 
    update(pos, val, (node << 1) + 1, mid + 1, y); 
    seg[node] = seg[node << 1] * seg[(node << 1) + 1]; 
    return; 
}
 
int query(int lo, int hi, int node, int x, int y) {
    if (lo > y || x > hi) return 1; 
    if (lo <= x && y <= hi) return seg[node]; 
    int mid = (x + y) >> 1; 
    int l = query(lo, hi, node << 1, x, mid); 
    int r = query(lo, hi, (node << 1) + 1, mid + 1, y); 
    return l*r; 
}
 
int main() {
    ios::sync_with_stdio(false); 
    cin.tie(NULL); 
    cout.tie(NULL); 
    
    while (cin >> n >> m) {
        for (int i = 1; i <= n; i++)
            cin >> a[i]; 
 
        init(1, 1, n); 
        while (m--) {
            char inp; int x, y; 
            cin >> inp >> x >> y;
            if (inp == 'C') 
                update(x, y, 1, 1, n);
            else if (inp == 'P'){
                int ans = query(x, y, 1, 1, n);
                if (ans == 0)
                    cout << '0';
                else if (ans > 0)
                    cout << '+';
                else if ( ans < 0)
                    cout << '-'; 
            }
        }
        cout << '\n'; 
    }
    return 0; 
}


저작자표시

'PS) BOJ > Segment Tree' 카테고리의 다른 글

[C++] 커피숍2 [백준 1275]  (0) 2018.08.17
[C++] 커피숍2 [백준 1275]  (0) 2018.08.16

+ Recent posts

티스토리툴바