[C++] 커피숍2 [백준 1275]

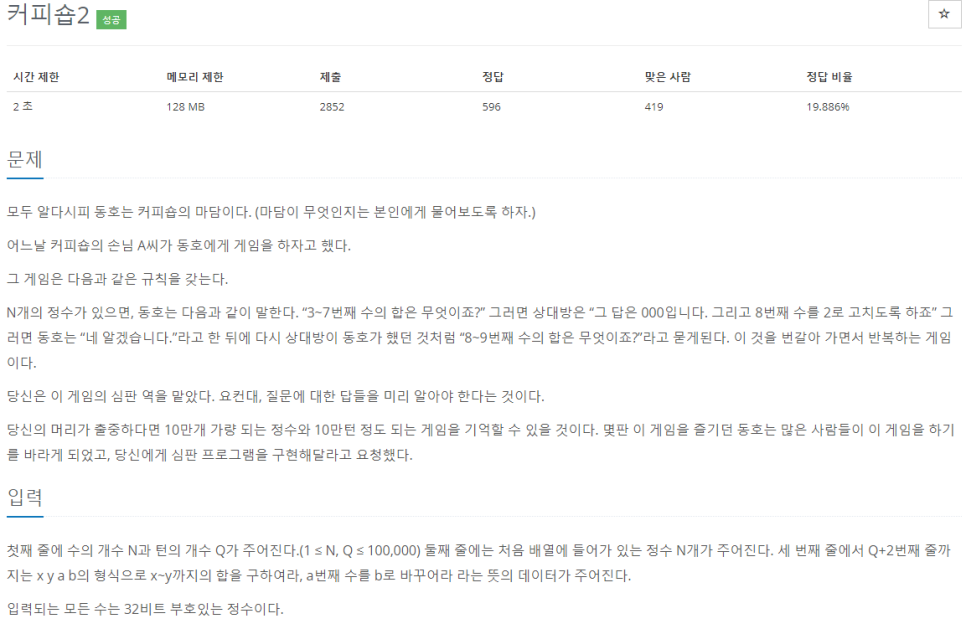
전형적인 세그먼트 트리 문제인데 함정은 쿼리에 무조건 작은수~큰수라는 조건이 없으므로 
조건으로 잘 처리해주면 금방 풀수 있는 문제이다. 
바텀업 세그먼트 트리를 구현해서 풀었다. 

구간합 구하기 문제는 역시 세그먼트 트리 구현해서 푸는게 짱인거같다...
(내가 아는선에서는... ㅎ)

시간복잡도는 M*NlogN 만큼 소요되는것같다. 
주어지는 쿼리의 수가 10만턴정도이니 입출력을 줄여주는것도 시간을 충분히 줄여준다. 

참고로 덧셈과정에서 정수형을 넘어갈수 있으니 long long을 사용했다.

https://www.acmicpc.net/problem/1275

1275번: 커피숍2

1275번 제출 맞은 사람 숏코딩 풀이 풀이 작성 풀이 요청 재채점/수정 채점 현황 강의 커피숍2 시간 제한 메모리 제한 제출 정답 맞은 사람 정답 비율 2 초 128 MB 2852 596 419 19.886% 문제 모두 알다시피 동호는 커피숍의 마담이다. (마담이 무엇인지는 본인에게 물어보도록 하자.) 어느날 커피숍의 손님 A씨가 동호에게 게임을 하자고 했다. 그 게임은 다음과 같은 규칙을 갖는다. N개의 정수가 있으면, 동호는 다음과 같이 말한다. “3~7번째 수의 합은 무엇이죠?” 그러면 상대방은

www.acmicpc.net

<Code>

//pda_pro12
#include<algorithm>
#include<iostream>
 
#define N_ 100000
#define INT 0x7fff0000
 
using namespace std; 
 
typedef long long ll;
ll a[N_], seg[N_ * 4], n, q; 
 
void init(int node, int x, int y) {
    if (x == y) {
        seg[node] = a[x]; 
        return; 
    }
    int mid = (x + y) >> 1; 
    init(node << 1, x, mid); 
    init((node << 1) + 1, mid + 1, y); 
    seg[node] = seg[node << 1] + seg[(node << 1) + 1];
    return; 
}
 
void update(int pos, int val, int node, int x, int y) {
    if (pos < x || pos > y) return; 
    if (x==y) {
        seg[node] = val; 
        return; 
    }
    ll mid = (x + y) >> 1; 
    update(pos, val, node << 1, x, mid); 
    update(pos, val, (node << 1) + 1, mid + 1, y); 
    seg[node] = seg[node << 1] + seg[(node << 1) + 1]; 
    return; 
}
 
ll query(int lo, int hi, int node, int x, int y) {
    if (lo > y || hi < x) return 0; 
    if (lo <= x && y <= hi) return seg[node]; 
    ll mid = (x + y) >> 1; 
    ll l = query(lo, hi, node << 1, x, mid); 
    ll r = query(lo, hi, (node << 1) + 1, mid + 1, y);
    return l+r; 
}
 
int main() {
    ios::sync_with_stdio(false); 
    cin.tie(NULL); 
    cout.tie(NULL); 
 
    cin >> n >> q; 
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    init(1, 1, n); 
    while (q--) {
        int a, b, c, d; 
        cin >> a >> b >> c >> d;
        int a1 = (a > b) ? b : a; int b1 = (a > b) ? a : b; 
        cout << query(a1, b1, 1, 1, n) << '\n'; 
        update(c, d, 1, 1, n);
    }
    return 0; 
}