이 포스팅을 보고 많은분들이 LIS에 대해서 아! 하시고 창을 닫으시길 바라며
포스팅을 해보겠습니다.
물론 제가 올린 내용중 문제가 되는 부분이 있다면 언제든지 댓글로 남겨주시면 환영입니다!
( 필자는 아직 좁밥이므로 갓들의 지적속에 자라나고 있습니다 )
n사이즈의 배열에서 일부 원소들을 뽑아내어 부분수열을 만들어 내었을때
증가하는 수열이 되도록 할때, 가장 긴 길이를 구하는 문제를 LIS라고 합니다.
Dynamic Programming에서 빈번하게 등장하는 문제로 알고있으며 실제로 감소하는 수열도 존재합니다.
예를 들어 [5, 2, 3, 7, 4, 1] 이라는 배열이 있다고 해보겠습니다.
먼저 이 배열에서 가장 긴 증가하는 부분수열을 뽑아낸다고 한다면, [2, 3, 4,]를 뽑아낸
길이 3이 LIS의 길이가 됩니다.
문제에 대한 설명에 앞서
인덱스 트리 풀이법, N^2풀이법, lower_bound 풀이법 등 다양한 방법이 존재하지만 필자가 알고있는
N^2 풀이법과 Lower_bound를 사용한 선형시간으로 푸는 방법에 대하여 설명하도록 하겠습니다.
그렇다면 N^2의 풀이를 먼저 사용하여
풀이해보겠습니다.
1. N^2을 사용해보자
N^2을 사용하기 위해서는 일반적으로 N사이즈가 1000 정도에서 빈번하게 사용되고 있습니다.
그렇다면 N^2의 풀이는 어떤 풀이길래?????
위와 같은 수열이 있다고 생각해보자
원본배열 arr[]에 위 값들을 저장해두고
입력과 동시에 자기자신은 길이 1을 가지고 있으므로
원본과 같은사이즈의 배열 dp[i] (value가 있는 index번째에) 1로 초기화 해주도록 하자
자 그러면 이제 원본의 1번째부터 n번째까지 핀을 꽂으면서 그 앞쪽을 탐색해본다고 따저보자
이게 이해가 되지 않는다면 아래 그림을 참고해보자
핀을 꽂은 위치를 기준으로 앞쪽을 전부 탐색해보는것이다. 이짓을 왜하냐?
왜냐하면 핀을 꽂은 위치가 자신보다 앞쪽 인덱스에 위치한 value가 작다면, 즉 (증가수열을 이룰수도 있는 부분이라면!)
-> 내가 앞쪽에 있는 값보다 크다면 당연히 증가수열이지 않은가
그렇다면 해당 인덱스에 저장된 DP테이블값을 보는것이다!
즉, dp테이블에 저장된 데이터의 의미는 엄밀히 말하면
(i번째까지 핀을 꽂으면서 탐색을 해보았을 때 가장 긴 LIS의 길이만 저장되어있는것이다.)
(가장 중요한건 i번째까지만!!! 계산했을때이다. )
위그림은 핀을 꽂은 순서에 따라서 DP테이블에 저장된 LIS의 길이를 저장한것이다. 이 테이블 내의 값과 과정이 이해가 된다면
N^2에 대한 이해는 완벽히 되었다고 볼수 있다.
이제 지금까지 설명해본 논리를 종합해보자
1. 원본을 기준으로 DP테이블을 갱신해 나간다고 생각하는것이 바탕되어있다.
2. 원본 1번째부터 N번째까지 그 앞쪽의 인덱스들을 무식하게 전부 봐주는 방식인데
원본 현 인덱스보다 작다면(증가수열이 가능하므로) 해당 인덱스의 DP테이블에
저장된VALUE+1을했을때 기존에 저장되어있던 값보다 크다면
갱신해주고 아니라면 SKIP해준다.
3. 그럼 이제 그 과정에서 즉 항상 맨마지막 인덱스가 LIS값이 저장되어있다는 보장이 없으므로
매번 기준이 되는 원본 인덱스에서의 DP값들 중의 최대값이 LIS이므로
max값만 갱신해주며 쭉 끝까지 탐색하면 된다~
자 이제 Lower_bound를 활용한 좀더 큰 사이즈의 배열의 LIS를 구해보자
이 풀이는 선형시간, 즉 O(n)으로 해결할 수 있는 풀이이다. 그렇다면 O(n)으로 어떻게 해결할 수 있나?
Lower_bound (이분탐색 기반의 해당 value 이상의 값이 최초로 등장하는 인덱스의 위치를 찾아내는 알고리즘이다)
을 사용하여 value 이상이 등장하는 위치를 찾아준다.
먼저 위와 같은 똑같은 원본배열로 설명하겠다.
준비물은 정수형 벡터 하나와 lower_bound 알고리즘이면 된다.
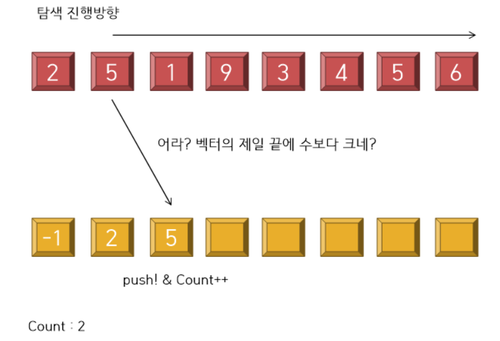
자 그렇다면 먼저 vector안에 -1을 넣고 시작한다.
물론 lis 문제가 자연수 문제일경우에만 해당된다.
(어떠한 수가와도 본인자체의 길이는 1이 되므로 )
여기서는 vector 컨테이너에 한번 넣을수 있다는 것이 어떠한 Event라고 생각해주면된다.
즉 vector에 보관되고 있는 수들은 기존에 갱신해왔던 lis길이를 구성하였었던 수들? 이라고 말하면 편하겠다.
그치만 lis가 3일때의 -> vector<int>에는 딱 이수들이 있어야겠지? 라는 말이 아니다.
위 그림을 가지고 과정을 설명해보겠다.
----------------------------------------------------<1 stage>----------------------------------------------------
----------------------------------------------------<2 stage>----------------------------------------------------
----------------------------------------------------<3 stage>----------------------------------------------------
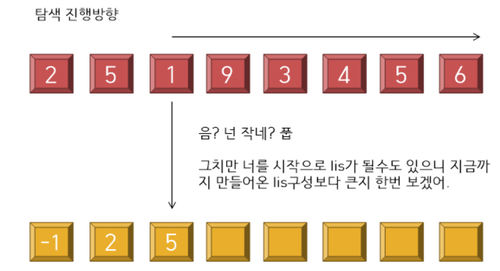
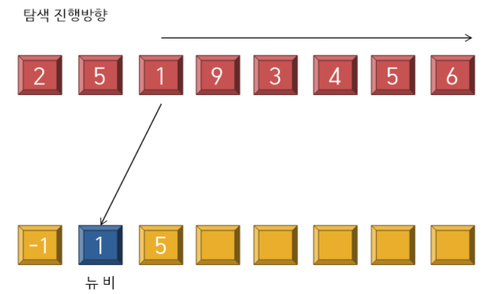
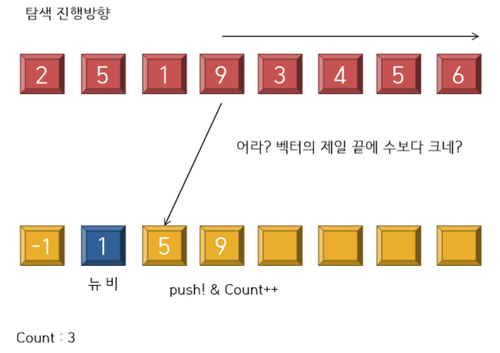
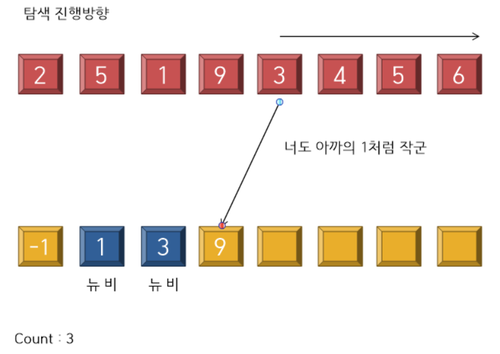
이 단계에서 어떤 로직이 일어날까? 그렇다 Lower_bound알고리즘을 사용하여
현 vector컨테이너에 저장된 수들(현존하는 lis 구성 체제라고 보는게 맞을것 같다 )
여기서 이 원본의 작은 수가 현 vector컨테이너에 들어왔을때 (어느 계급??)인지를
보는게 맞을것같다.
이때 사용되는 Lower_bound알고리즘의 복잡도는 O(LogN)이다
즉!!! 뒤에 등장한 작은수가 더 긴 lis수로 거듭날수 있는지 현체제의 해당 계급의 수와 1대1 매칭시켜가줘보는것이다.
( 사실 위에서 한말이 이 알고리즘 설명의 전부인것 같다 )
그렇다면 계속해서 구해보자. ( 이해가 안될땐 의심이 많아지기 때문이다 )
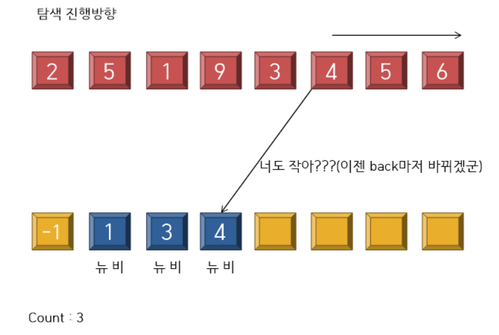
----------------------------------------------------<4 stage>----------------------------------------------------
짜잔~ 이렇게 바뀌엇다.
그럼이제 계속 더 잘 진행해보자
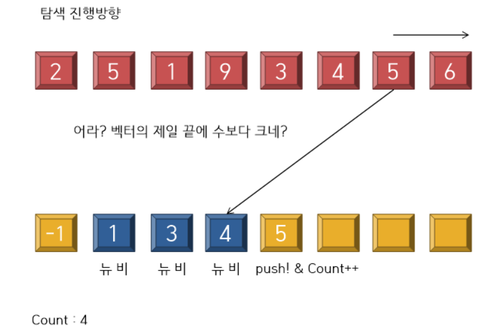
---------------------------------------------------- <5 stage> ----------------------------------------------------
---------------------------------------------------- <6 stage> ----------------------------------------------------
---------------------------------------------------- <7 stage> ----------------------------------------------------
---------------------------------------------------- <8 stage> ----------------------------------------------------
---------------------------------------------------- <9 stage> ----------------------------------------------------
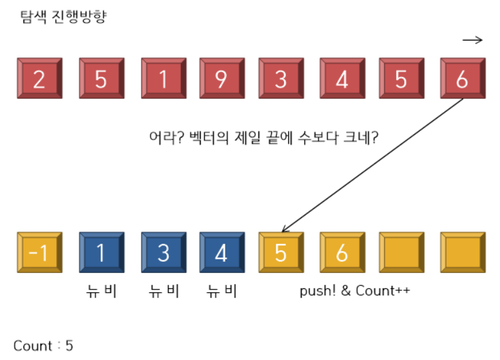
자 이렇게 하면 이제 count: 5를 마지막으로 종료가 되엇다.
저뒤에 어떠한 5나 6아 온다고 한들 back보다 작으므로 현수열의 back이 갱신될때까지의 인덱스는 기존 벡터
에도 5나 6이 잔존하니 길이가 갱신될리가 없는것은 자명하다.
파란색으로 칠한 인덱스는 Lower_bound를 통해 갱신된 것을 표시한것이다.
총 lower_bound함수호출 3번, 탐색은 1방향으로 O(N)이 이루어졌다.
즉 NLogN정도?의 복잡도가 발생하는것 같다
< 연습 문제 >
https://www.acmicpc.net/problem/11053
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | //2018年 08月 15日 LIS //pda_pro12 #include<iostream> #include<algorithm> #define N_ 1001 using namespace std; int dp[N_], a[N_], n, m, ans; int main() { ios::sync_with_stdio(false); cin.tie(NULL), cout.tie(NULL); cin >> n; for (int i = 1; i <= n; i++) cin >> a[i], dp[i] = 1; for (int i = 1; i <= n; i++) { for (int j = 1; j < i; j++) { if (a[i] > a[j]) dp[i] = max(dp[i], dp[j] + 1); ans = max(ans, dp[i]); } } cout << dp[n]; return 0; } |
<Code> - (Lower_bound 풀이법)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | //2018年 08月 15日 LIS //pda_pro12 #include<iostream> #include<algorithm> #include<vector> #define N 1000001 #pragma warning(disable:4996) using namespace std; int n, m, a[N], ans; vector<int> v(n); int main() { ios::sync_with_stdio(false); cin.tie(NULL), cout.tie(NULL); cin >> n; for (int i = 1; i <= n; i++) cin >> a[i]; v.push_back(-1); for (int i = 1; i <= n; i++) { if (v.back() < a[i]) { ans++; // ans가 counting 해주는 것은 back을 갱신하는 순간이 몇번이엇는지 (즉 현재까지 세어온 LIS의 길이를 갱신해주었던 순간의 횟수를 세어주는 것이다 ) v.push_back(a[i]); } else { auto j = lower_bound(v.begin(), v.end(), a[i]); // a[i]이상의 값이 등장하기 시작하는 인덱스의 위치를 찾는다 *j = a[i]; // a[i]로 해당 lower_bound번째의 인덱스를 수정해주므로 이 값은 이제 } } cout << ans; return 0; } |